排序算法

memcpy

完成内存的拷贝
- 如果内存有重叠（对小端），则从高位到低位复制
- 如果内存无重叠，则从低位到高位传递

  void* my_memcpy(void *dst, void *src, size_t count){
    if(dst == nullptr || src == nullptr){
      return nullptr;
    }
    char* temp_dst = (char*) dst;
    char* temp_src = (char*) src;
    if(temp_dst > temp_src && temp_dst < temp_src+ count){
      // 内存重叠
      temp_dst = temp_dst + count -1;
      temp_src = temp_src + count -1;
      while(count--){
        *temp_dst-- = *temp_src--;
      }
    }
    else {
      while(count--){
        *temp_dst++ = *temp_src++;
      }
    }
    return (void * )dst;
  }

排序算法

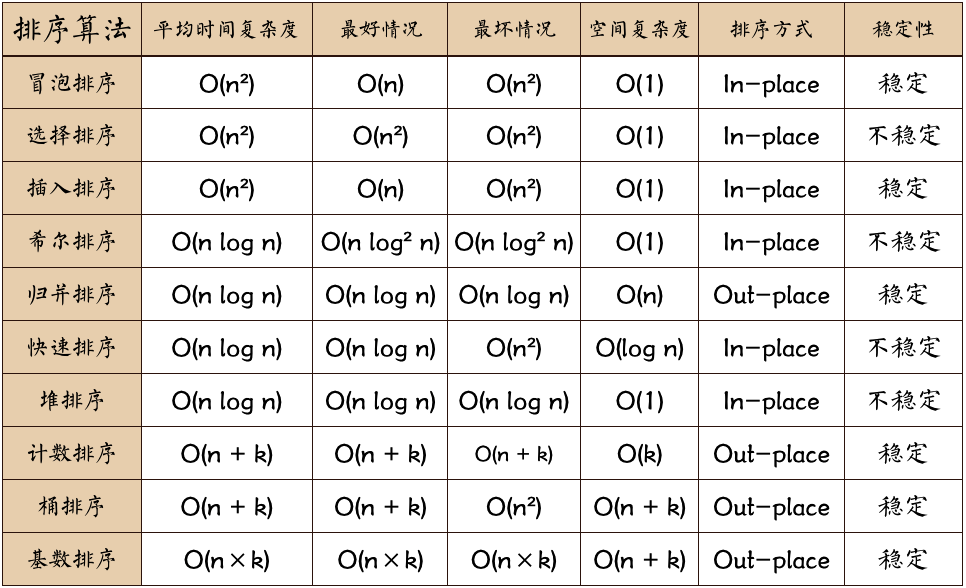
排序算法比较

插入排序

直接插入排序：复杂度O(n^2)

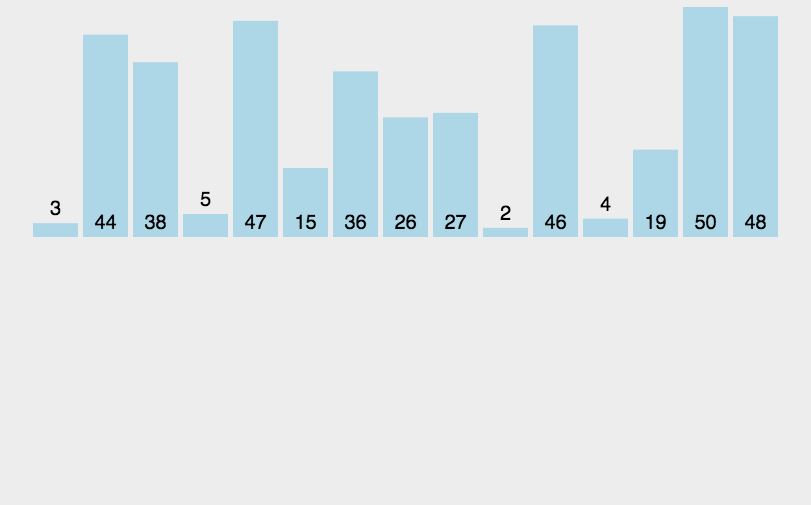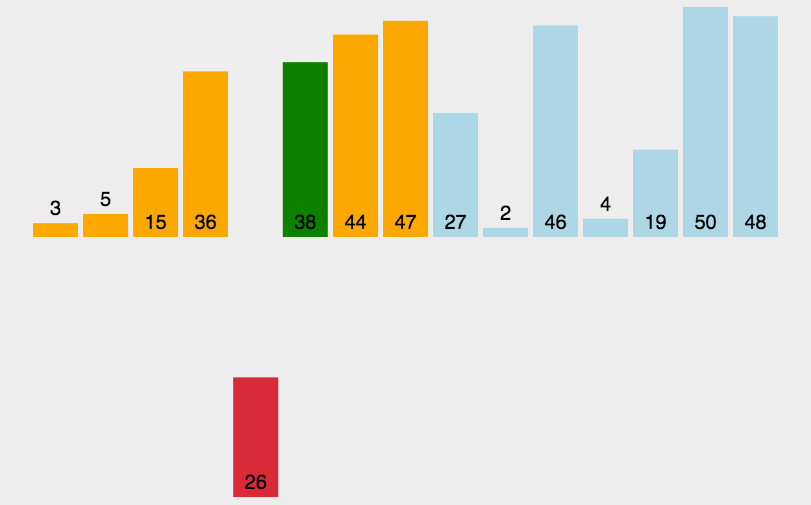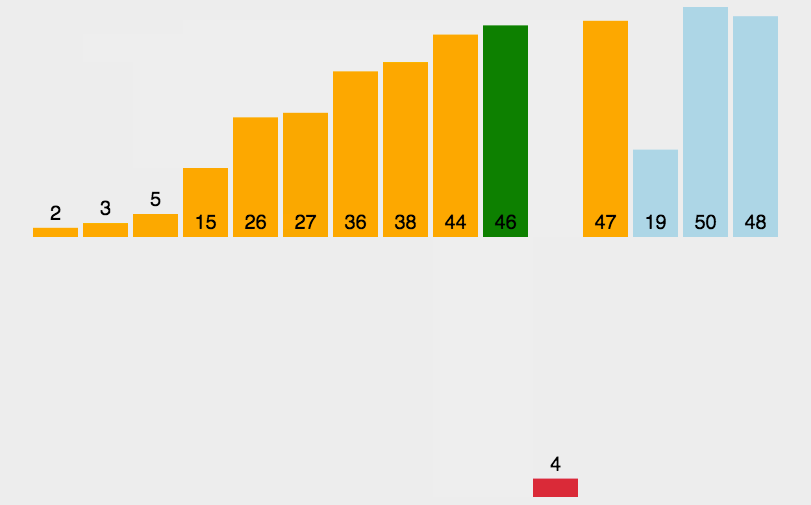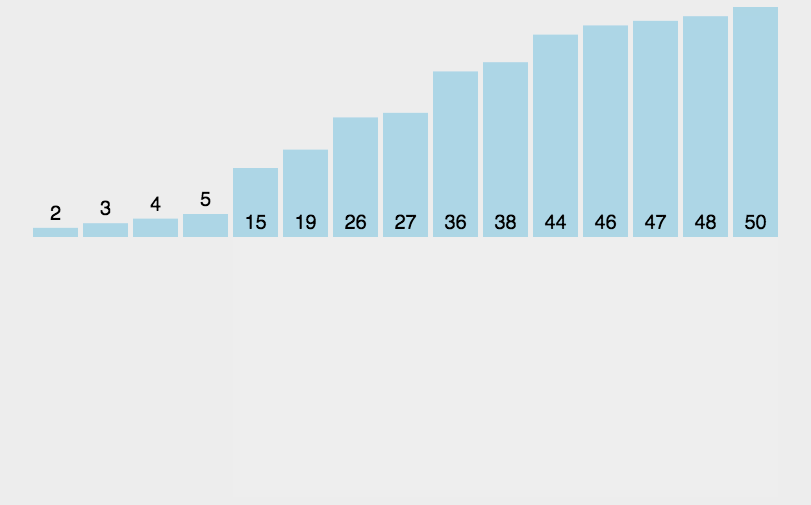
原理

将无序元素一个一个插入到有序部分中
- 对于待排序元素temp = index.1:length-1，寻找其左侧有序序列index.0:temp-1的插入位置
- 对index从 temp-1 到 0 过程中
  - temp > index值
    - a[index+1] = temp
  - temp < index值（如果没有到头部）
    - 在下一次处理(a[index+1] = a[index])
  - temp < index值（在头部）
    - 本次处理 a[index] = temp;

伪码

  // 待排序数组
  for(index_1 := 1:length-1):
   // 将待排序元素取出
    temp = a[index_1]
    // 排序位置index
    for(index_2 := index_1:0):
    // for循环执行之后的下一次处理
      a[index_2+1] = a[index_2];
      // 如果可以放入
      if(temp > a[index_2]){
        a[index_2 + 1] = temp;
      }
      // 对于头部的处理
      if(temp < a[index_2] && index_2 ==0){
        a[index_2] = temp;
      }

      

代码

  void straight_inserting_sort(int a[], int length){
    // 对所有待排序元素来说
    for(int i = 1; i <length; i++){
      // 如果比排好序的序列的最大值小
      if(a[i] < a[i-1]){
        int temp = a[i];
        // 从序列最大值遍历排好序的序列[0,i-1]
        for(int j = i - 1; j >=0 ; j--){
          a[j + 1] = a[j];

          // 如果找到该位置
          if(a[j] < temp){
            a[j+1] = temp;
            break;
          }
          // 如果该值最小
          if(a[j] > temp && j == 0 ){
            a[j] = temp;
          }
        }
      }
    }
  }

折半插入排序

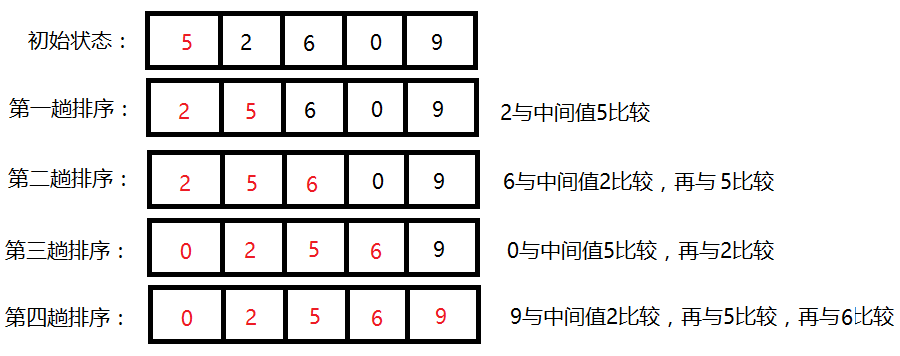
将右侧数组的元素逐个插入到左侧排好序的数组
确定排好序数组的ordered_index := 0:index-1
利用二分搜索查找插入点index+1 >temp
将index右侧所有值均右移一位
将值赋值到index+1位置

伪码

  for(index := 1:length-1){
    temp = a[index];
    left = 0, right = index -1
    while(left <= right){
      mid = left + (right-left) /2;
      if(a[mid] > temp){
        right = mid-1
      }
      else{
        left = mid+1;
      }
      
    }
    for(right右侧){
      全部右移一位
    }
    值赋值
  }

  void binary_insert_sout(int a[], int length){
    int low, high, mid;
    for(int i = 1 ; i <length ; i++){
      low = 0;
      high = i - 1;
      temp = a[i];
      while(high >=low){
        mid = low+ (high - low) /2;
        if(temp < a[mid]){
          high = mid -1;
        }
        else {
          low = mid +1;
        }
      }
      // 选择high而不是low的原因：
      for(int j =i - 1 ; j > high ; j--){
        a[j+1] = a[j];
      }
      a[j+1] = temp;
    }
  }

冒泡排序：O(n^2)

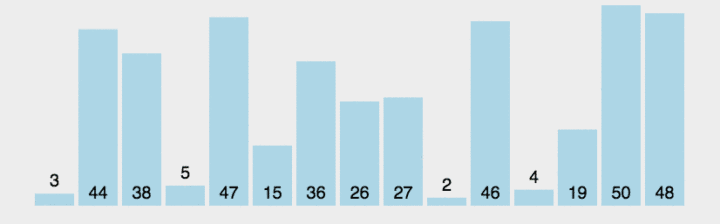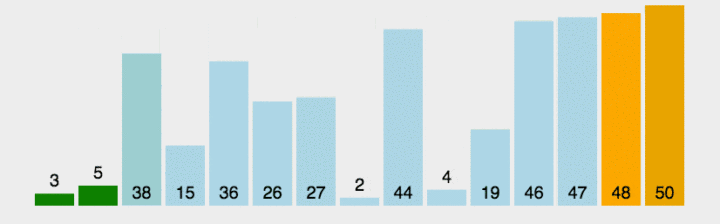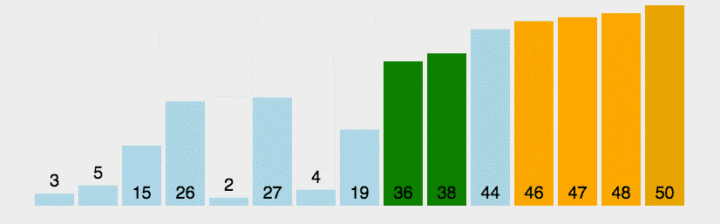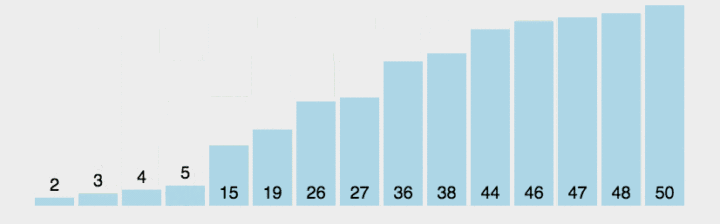
冒泡排序每次都会将最大值放在数组末尾

  void bubble_sort(int a[], int length){
    for(int i = 0; i  <length -1; i++){
      for(int j = 0; j < length - i-1; j++){
        if(a[j] >a[j+1]){
          int temp = a[j];
          a[j] = a[j+1];
          a[j]+1 = temp;
        }

      }
    }
  }

选择排序：O(n^2)

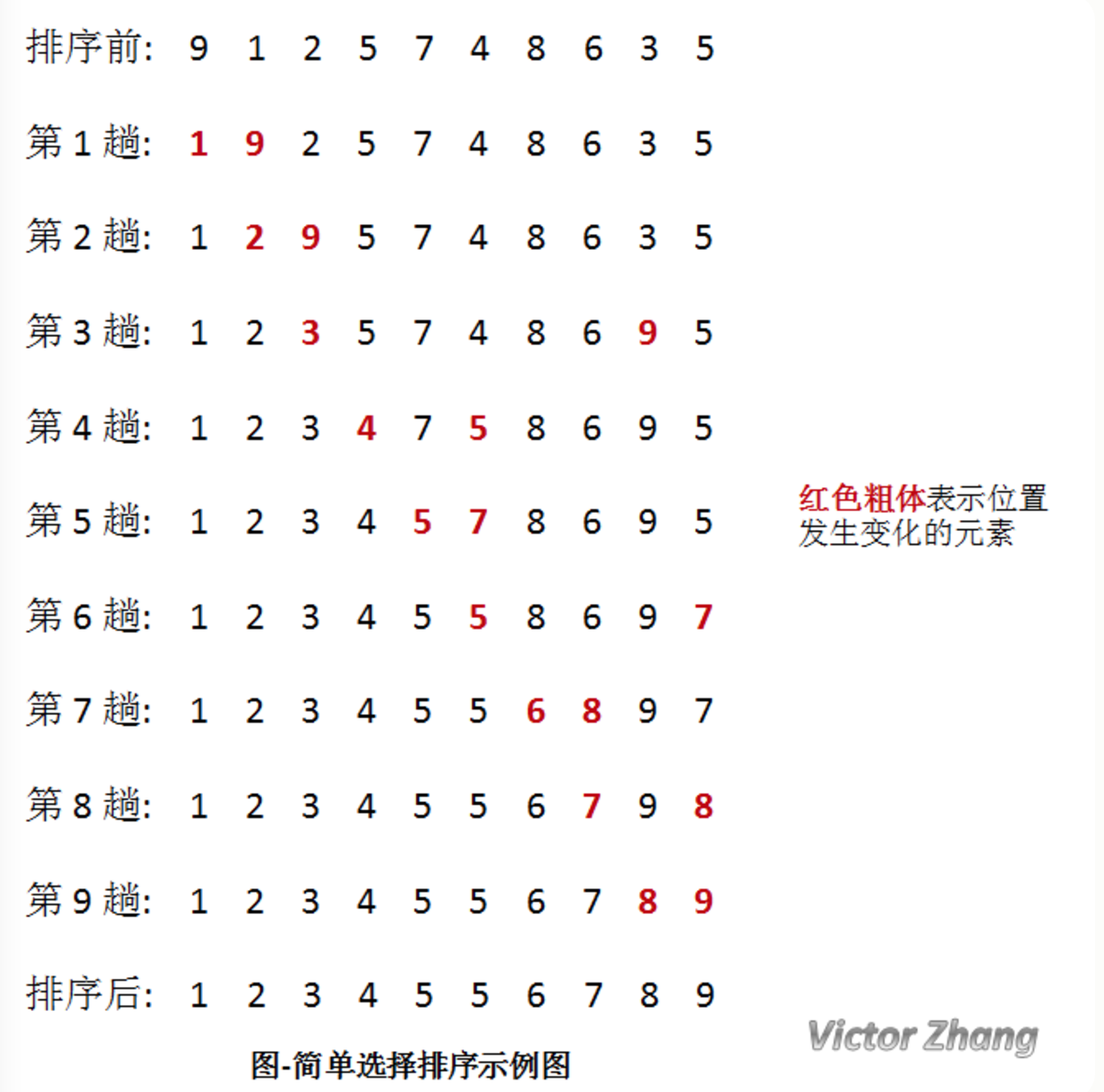
  void select_sort(int a[], int length){
    for(int i = 0; i <length-1; i++){
      int min_index = i;
      for(int j = i+1; j <length; j++){
        if(a[min_index] >a[j]){
          min_index = j;
        }
      }
      if(i != min_index){
        int temp = a[i];
        a[i] = a[min_index];
        a[min_index] = temp;
      }
    }
  }

希尔排序：O(nlogn)

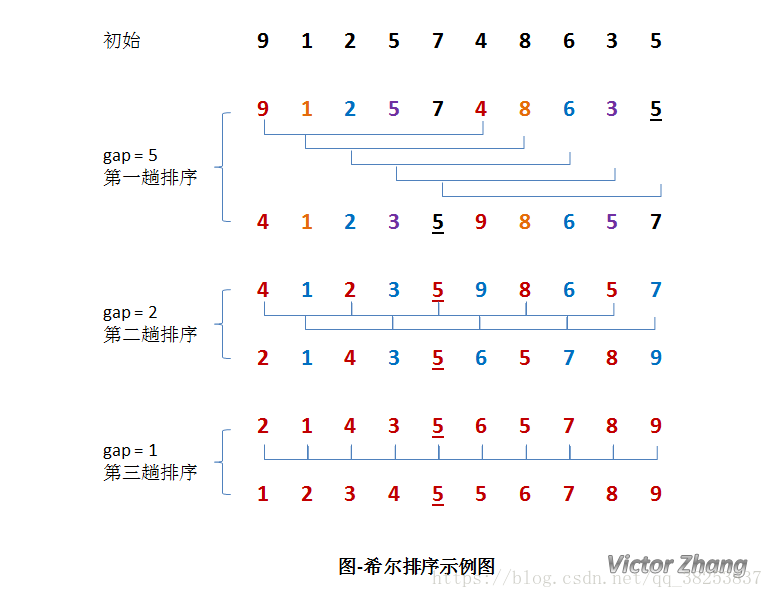
  void shell_sort(int a[], int length){
    int i, j, gap;
    for(gap = length/2; gap >0; gap /=2){
      for(i = 0; i < gap; i++){
        for(j = i + gap; j < length; j += gap){
          int temp = a[j];
          k = j - gap;
          while(k >=0 && a[k] > temp){
            a[k + gap] = a[k];
            k -= gap; 
          }
          a[k + gap] = temp;
        }
      }
    }
  }

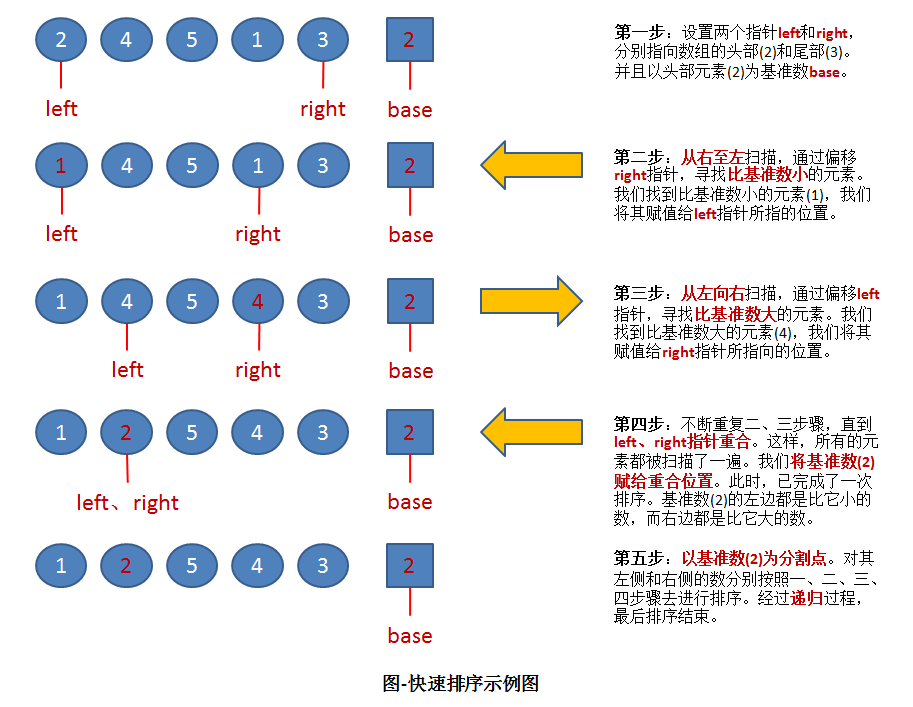
快速排序：O(nlogn)

  void quick_sort(int[] a, int low, int high){
    if(low < high){
      int key = quick_sort_index(a, low, high);
      quick_sort(a, low, key-1);
      quick_sort(a, key+1, high);
    }
  }

  int quick_sort_index(int[] a, int low, int high){
    int temp = a[low];
    int rightvalue;
    int leftvalue;
    while(low < high){
      while(low < high && a[high] >= temp){
        high--;
      }
      a[low] = a[high];
      while(low < high && a[low] <=temp){
        low++;
      }
      a[high] = a[low];
    }
    a[low] = temp;
    return low;
  

  }

堆排序：O(nlogn)

步骤

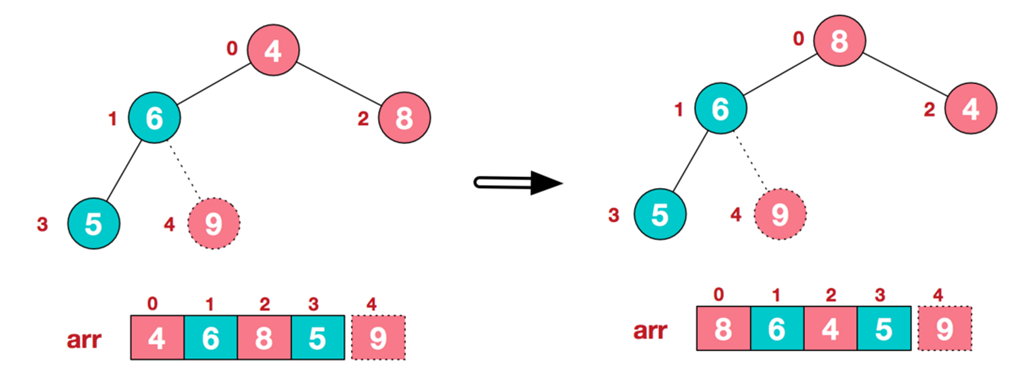
无序序列建立完全二叉树
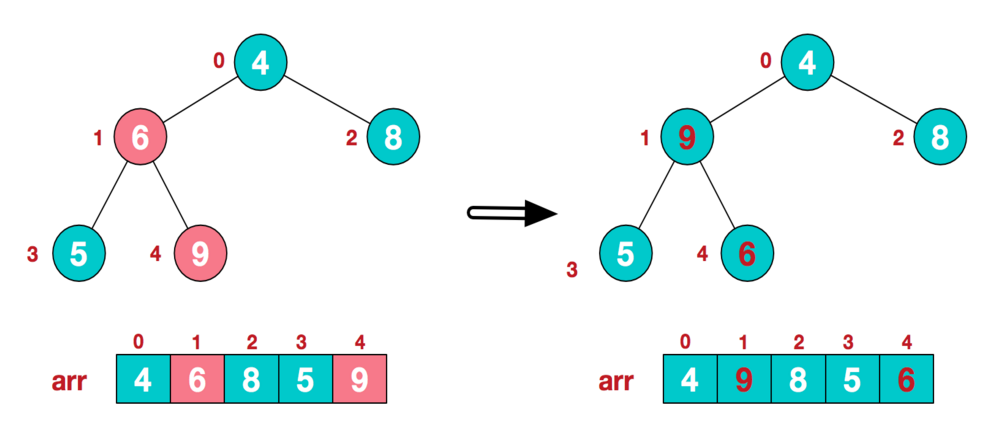
从最后一个叶子节点开始，从左到右，从下到上调整，将完全二叉树调整为大根堆
- 找到第1个非叶子节点6，由于6的右子节点9比6大，所以交换6和9。交换后，符合大根堆的结构
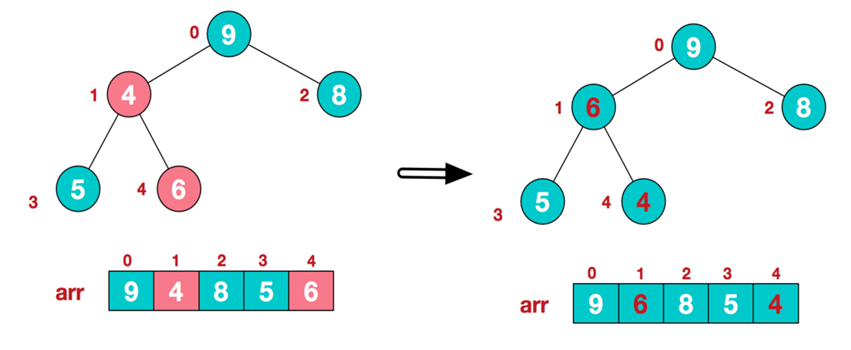
- 找到第2个非叶子节点4，由于的4左子节点9比4大，所以交换4和9。交换后不符合大根堆的结构，继续从右到左，从下到上调整。
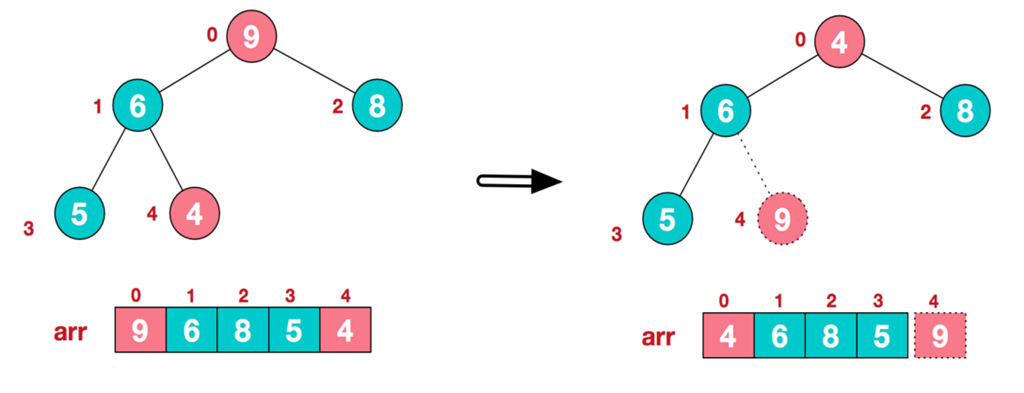
交换堆元素（交换堆首和堆尾元素–获得最大元素）
重建大根堆（前n-1个元素）
重复执行步骤二和步骤三，直到整个序列有序图

  void heap_sort(vector<int>& arr, int length){
    for(int i = length/2 -1; i>=0 ; i++){
      adjust(arr, length, i);
    }
    for(int i = size -1; i>=0 ; i--){
      swap(arr[0], arr[i]);
      adjust(arr, i, 0);
    }
  }

  void adjust(vector<int>& arr, int length, int index){
    int left = 2*index + 1;
    int right = 2*index +2;
    int maxindex = index;
    if(left < length && arr[left] > arr[maxindex])  maxindex = left;
    if(right< length && arr[right] > arr[maxindex]) maxindex = right;

    if(maxindex != index){
      swap(arr[maxindex], arr[index]);
      adjust(arr, length, maxindex);
    }
  }

  void swap (int value1, int value2){
    int temp = value1;
    value1 = value2;
    value2 = temp;
  }

归并排序：O(nlogn)

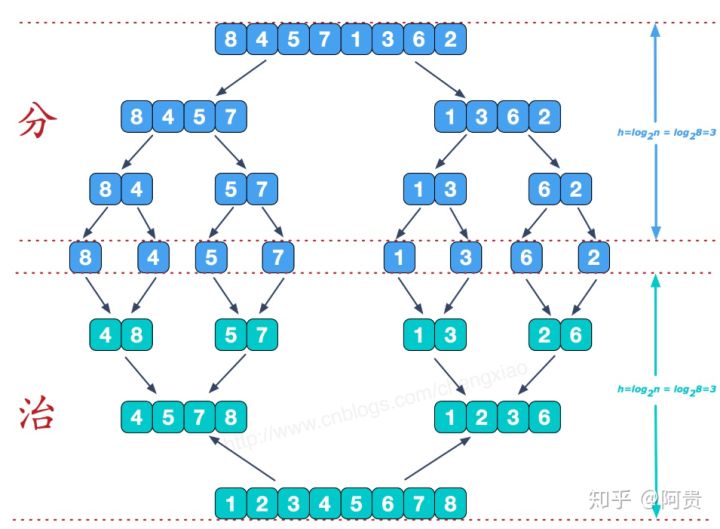
  void merge_sort(int[] a, int low, int high){
    if(low < high){
      int mid = low + (high - low) / 2;
      merge_sort(a, low, mid);
      merge_sort(a, mid+1, high);

      merge(a, low, mid, high);
    }

  void merge(int[] a, int low, int mid, int high){
    int i = low;
    int j = mid +1;
    k = 0;
    int* temp = new[high - low - 1];
    while(i <=mid && j <= high){
      if(a[i] <= a[j]){
        temp[k++] = a[i++];
      }
      else {
        temp[k++] = a[j++];
      }
    }
    while(i<=mid){
      temp[k++] = a[i++];
    }
    while(j <= high){
      temp[k++] = a[j++];
    }
    for(i = low, k = 0; i<= high; i++,k++){
      a[i] = temp[i];
    }
    delete[] temp;
  }
  }

计数排序O(n+k)

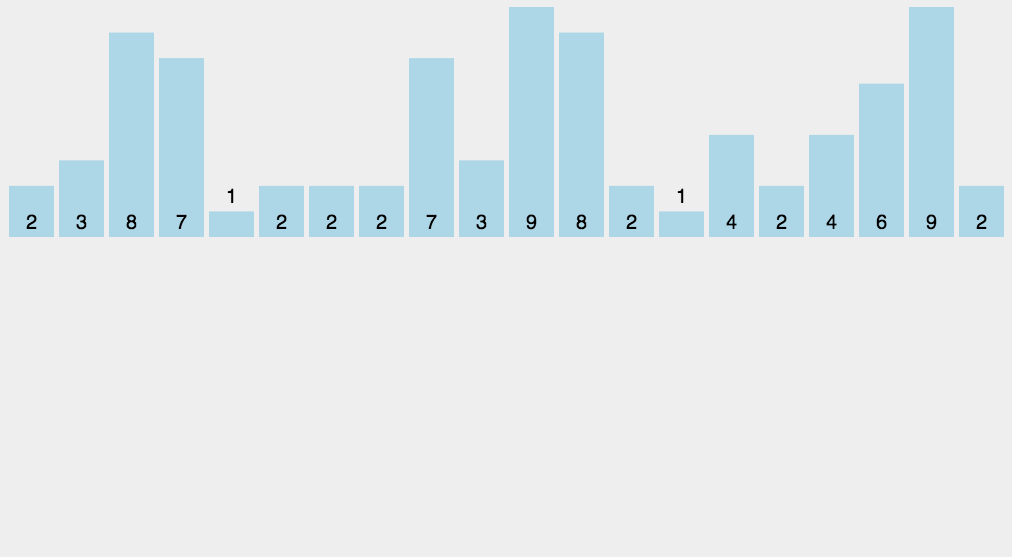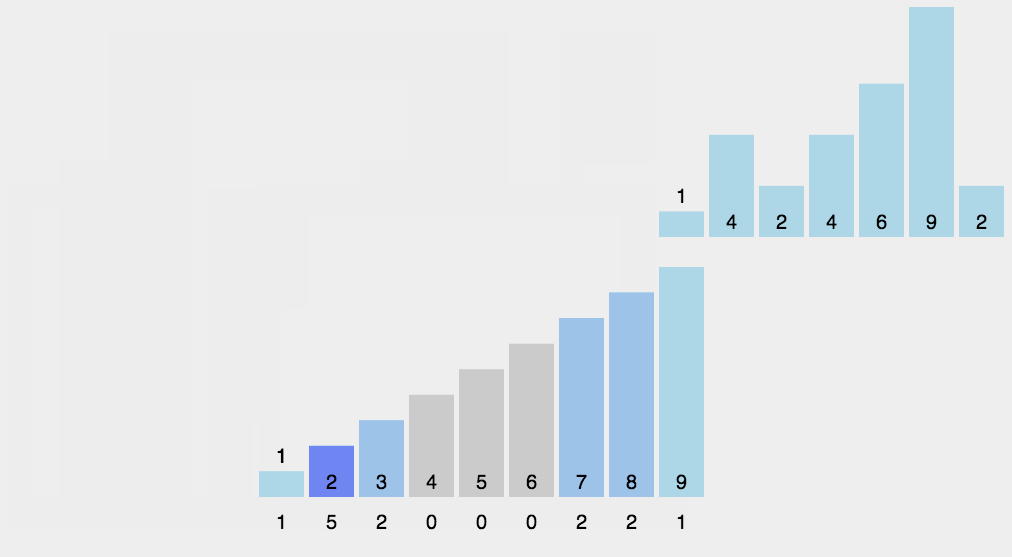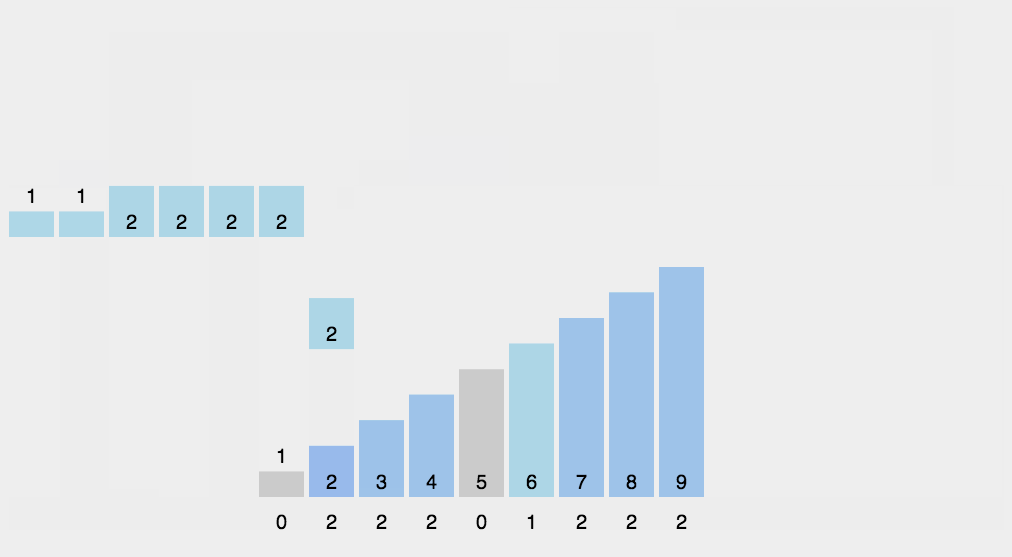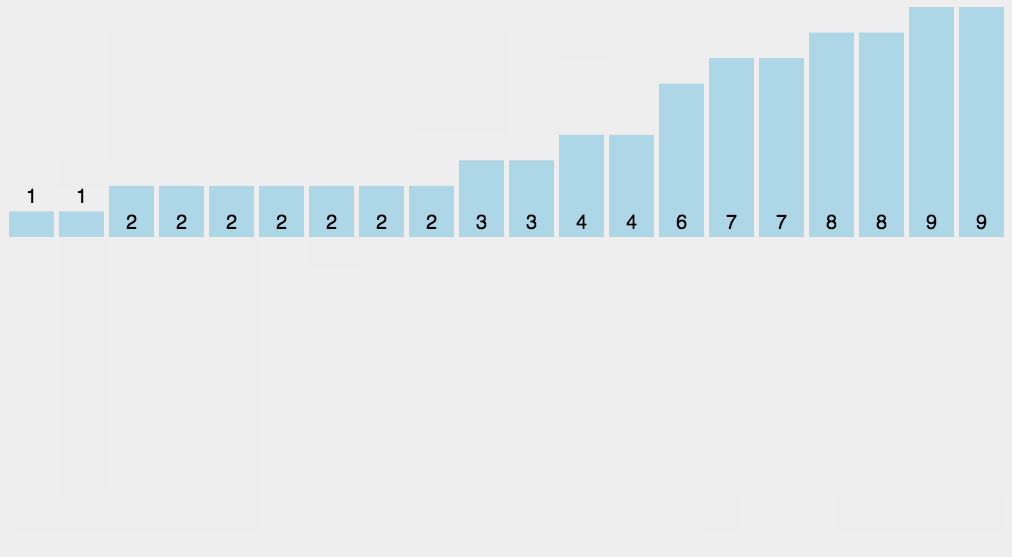
  void count_sort(int[] a, int length){
    int max = a[0];
    int i = 0;

    while( i< length -1){
      max = (a[i] > a[i+1]) ? a[i]: a[i+1];
      i++;
    }
    int* countArray = new int[max+1]{0};
    int* temp = new int[length];

    for(int i = 0; i < length; i++){
      countArray[a[i]]++;
    }
    // 特别注意此方法实现，可以减少复杂度
    for(int i = 1; i < length + 1; i++){
      countArray[i] += countArray[i-1];
    }
    // 反向遍历
    for(int i = length-1; i >= 0 ; i--){
      temp[countArray[a[i]]-1] = a[i];
      countArray[a[i]]--;
    }

    for(int i = 0 ; i < length; i++){
      a[i] = temp[i];
    }
    delete[] countArray;
    delete[] temp;
  }

基数排序O(n*k)

  int get_max_digits(int[] a, int length){
    int max = a[0];
    int i = 0;
    while(i < length-1){
      max = (a[i] > a[i+1]) ? a[i]: a[i+1];
    }
    int b =0;
    while(max > 0){
      b++;
      max /= 10;
    }
    return b;
  }

  void sort(int[] a, int length){
    int d = get_max_digits(a, length);
    int* temp = new int[length];
    
    int padding = 1;
    for(int i = 0; i < d; i++){
      int count[10]={0};
      
      for(int j = 0; j <length; j++){
        int tail_number = (a[j]/padding) % 10;
        count[tail_number]++;
      }

      for(j = 1; j <10; j++){
        count[j] += count[j-1];
      }

      for(int j = length-1; j >=0; j--){
        int tail_number = (a[j] / padding) % 10;
        temp[count[tail_number] - 1] = a[j];
        count[tail_number]--;
      }
      for(int j = 0; j < length;j++){
        b[j] = temp[j];
      }
      radix *= 10;
    }
    delete[] temp;
  }

桶排序：O(n+k)

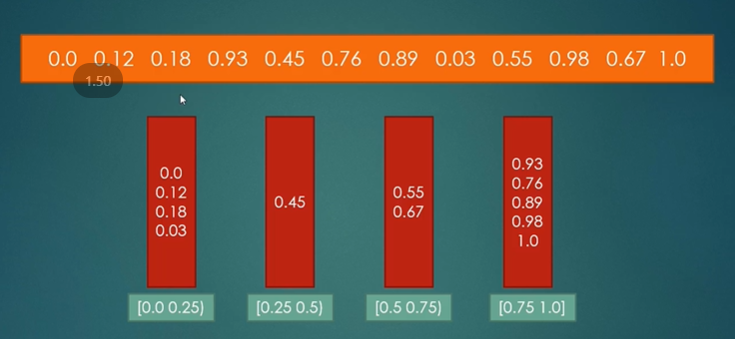
  void bucket_sort(int[] a, int length){
    int max = INT_MIN;
    int min = INT_MAX;

    for(int i = 0; i <length; i++){
      if(a[i] > max) max = a[i];
      if(a[i] < min) min = a[i];
    }

    int bucket_len = max - min +1;
    int bucket[bucket_len];
    for(int i = 0; i < bucket_len; i++){
      bucket[i] = 0;
    }

    int index = 0;
    for(int i = 0 ; i < length ; i++){
      index = arr[i] - min;
      bucket[index]++;
    }
    int start = 0;
    for(int i = 0; i< bucket_len; i++){
      for(int j = start; j < start + bucket[i]; j++){
        a[j] = min + i;
      }
      start += bucket[i];
    }
  }

上篇设计模式

下篇数据结构