特殊数据结构

AVL树

节点定义

  template<class T>
  class AVLTreeNode{
    public:
      T key;
      int height;
      AVLTreeNode *left;
      AVLTreeNode *right;
      AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r): key(value), left(l), right(r){}
  }

树的类

  template<class T>
  class AVLTree{
    private:
      AVLTreeNode<T>* root;
    public:

      AVLTree();
      ~AVLTree();

      int height();
      int max(int a, int b);

      void preOrder();
      void inOrder();
      void postOrder();

      AVLTreeNode<T>* search(T key);
      AVLTreeNode<T>* iterativeSearch(T key);
      T minimum();
      T maximum();
      void insert(T key);
      void remove(T key);
      void destroy();
      void print();
    private:
      // 内部接口 
      // 获取树的高度
      int height(AVLTreeNode<T> *tree);
          
      // 前序遍历
      void preOrder(AVLTreeNode<T> *tree) const;
          // 中序遍历
      void inOrder(AVLTreeNode<T> *tree) const;
          // 后序遍历
      void postOrder(AVLTreeNode<T> *tree) const;
          
      // （递归实现）查找AVL树中键值为key的结点
      AVLTreeNode<T>* search(AVLTreeNode<T> *x, T key) const;
      // （非递归实现）查找AVL树中键值为key的结点
      AVLTreeNode<T>* iterativeSearch(AVLTreeNode<T> *x, T key) const;

      // 返回最小结点 
      AVLTreeNode<T>* minimum(AVLTreeNode<T> *tree);
      // 返回最大结点 
      AVLTreeNode<T>* maximum(AVLTreeNode<T> *tree);
          
      // 将结点插入到AVL树中
      AVLTreeNode<T>* insert(AVLTreeNode<T>* &tree, T key);
      // 删除结点，并返回被删除的结点 
      AVLTreeNode<T>* remove(AVLTreeNode<T>* &tree, AVLTreeNode<T> *z);
          
      // 销毁AVL树
      void destroy(AVLTreeNode<T>* &tree);
          
      // 打印AVL树
      void print(AVLTreeNode<T> *tree,T key,int direction);
          
      // LL：左左对应的情况(左单旋转)
      AVLTreeNode<T>* leftLeftRotation(AVLTreeNode<T> *k2);
      // RR：右右对应的情况(右单旋转)
      AVLTreeNode<T>* rightRightRotation(AVLTreeNode<T> *k1);
      // LR：左右对应的情况(左双旋转)
      AVLTreeNode<T>* leftRightRotation(AVLTreeNode<T> *k3);
      // RL：右左对应的情况(右双旋转)
      AVLTreeNode<T>* rightLeftRotation(AVLTreeNode<T> *k1);    
  };

树高度的实现

  template<class T>
  int AVLTree<T>::height(AVLTreeNode<T> *tree){
    // 不为null，返回树最大长度
    if(tree != nullptr){
      return tree->height;
    }
    // 为空树，则返回0
    return 0;
  }

  template<class T>
  int AVLTree<T>::height(){
    return height(root);
  }

旋转的实现

LL的单旋转

当插入或删除节点后，左子树仍然还有左节点，并导致AVL不平衡

  template<class T>
  AVLTreeNode<T>* leftLeftRotation(AVLTreeNode<T> *k2){
    AVLTreeNode<T> * k1;
    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;
    k2->height = max(height(k2->left), height(k2->right)) + 1;
    k1->height = max(height(k1->left), height(k1->right)) + 1;
  }

RR的单旋转

当插入或删除节点后，右子树仍然还有右节点，并导致AVL不平衡

  template<class T>
  AVLTreeNode<T>* rightRightRotation(AVLTreeNode<T> *k1){
    AVLTreeNode<T>* k2;
    k2 = k1->right;
    k1->right = k2->left;
    k2->left = k1;

    k1->height = max(height(k1->left), height(k1->right)) + 1;
    k2->height = max(height(k2->left), height(k2->right)) + 1;
  }

LR的双旋转

当插入或删除节点后，左子树仍然还有右节点，并导致AVL不平衡

  template<class T>
  AVLTreeNode<T>* leftRightRotation(AVLTreeNode<T> *k3){
    k3->left = rightRightRotation(k3->left);
    return leftLeftRotation(k3);
  }

RL的双旋转

当插入或删除节点后，右子树仍然还有左节点，并导致AVL不平衡

  template<class T>
  AVLTreeNode<T>* rightLeftRotation(AVLTreeNode<T> *k3){
    k3->right = leftLeftRotation(k3->right);
    return rightRightRotation(k3);
  }

插入的实现

  template<class T>
  AVLTreeNode<T>* insert(AVLTreeNode<T>* &tree, T key){
    if(tree == nullptr){
      tree = new AVLTreeNode<T>(key, NULL, NULL); 
    }
    else if(key < tree->key){
      tree->left = insert(tree->left, key);
      // 判断是否失去平衡
      if(key < tree->left->key){
        // 比左节点小，成为左节点的左节点
        leftLeftRotation(tree);
      }else{
        // 比左节点大，成为左节点的右节点，需要LR
        leftRightRotation(tree);
      }

    }
    else{
      tree->right = insert(tree->right, key);
      if(key > tree->right->key){
        // 比右节点大，成为右节点的右节点
        rightRightRotation(tree);
      }else{
        // 比右节点小，成为右节点的左节点，需要RL
        rightLeftRotation(tree);
      }
    }
  }

删除的实现

删除节点在叶子节点

删除只有一个左节点或右节点

删除有左右节点

  AVLTreeNode<T>* remove(AVLTreeNode<T>* &tree, AVLTreeNode<T> *z){
    if(tree == nullptr || z == nullptr){
      return nullptr;
    }
    if(z->key < tree->key){
      AVLTreeNode<T>* r = tree->right;
      tree->left = remove(tree->left, z);
      // 需要进行RL旋转
      if(r->left > r->right){
        tree = rightLeftRotation(tree);
      }else {
        tree = rightRightRotation(tree);
      }
    }
    else if(z->key > tree->key){
      AVLTreeNode<T>* l = tree->left;
      tree->right = remove(tree->right, z);
      // 需要进行RL旋转
      if(r->right > r->left){
        tree = keftRightRotation(tree);
      }else {
        tree = leftLeftRotation(tree);
      }
    }
    else{
      // 需要删除的节点
      if(tree->left !=null) && (tree->right != null){
        if(height(tree->left) > height(tree->right)){
          AVLTreeNode<T>* temp = maximum(tree->left);
          tree->key = temp->key;
          remove(tree->left, temp);
        }
        else{
          AVLTreeNode<T>* temp = minimum(tree->right);
          tree->key = temp->key;
          remove(tree->right, temp);
        }
      }
      else{
        AVLTreeNode<T>* temp = tree;
        tree = (tree->left !=null) ? tree->left:tree->right;
        delete temp;
      }
    }
    return tree;
  }

  template<class T>
  void AVLTree<T>::remove(T key)
  {
      AVLTreeNode<T> *z;
      if((z=search(root,key))!=NULL)
          root = remove(root,z);
  }

字典树

根节点不包含字符，除根节点外每一个节点都只包含一个字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

针对单词为：b，abc，abd，bcd，abcd，efg，hii得到的字典树

字典树宏

const int Num = 26;

字典树节点定义

struct TrieNode{
  bool is_word;
  TrieNode* next[Num];
  TrieNode() : is_word(flase){
    memset(next, NULL, sizeof(next));
  }
};

字典树定义

class Trie{
public: 
  Trie(){root = new TrieNode();}
  void insert(string word);
  bool search(string word);
  void deleteTrie(TrieNode* root);

private:
  TrieNode* root;
}

字典树方法

字典树插入方法

void Trie::insert(string word){
  TrieNode* location = root;
  for(int i = 0; i <word.size(); i++){
    if(location->next[word[i]- 'a'] == nullptr){
      TrieNode* temp = new TrieNode();
      location->next[word[i]- 'a'] = temp;
    }
    location = location->next[word[i] - 'a'];
  }
  location->is_word = true;
}

字典树寻找方法

bool Trie::search(string word){
  TrieNode* location = root;
  for(int i = 0 ; i < word.size() && location; i++){
    location = location->next[word[i] - 'a'];
  }
  return (location!= NULL && location->is_word);
}

字典树删除方法

  void Trie::deleteTrie(TrieNode* root){
    for(int i = 0 ; i < Num; i++){
      if(root->next[i] != NULL){
        deleteTrie(root->next);
      }
    }
    delete root;
  }

234树

红黑树

红黑树宏

enum Colour{
  RED,
  BLACK
} Color;

节点定义

template<typename Type>
struct RBTNode{
  Color color;
  Type key;
  RBTNode* left;
  RBTNode* right;
  RBTNode* parent;
};

红黑树定义

template<typename Type>
class RBTree{

public:
  RBTree(){
    Nil = BuyNode();
    root = Nil;
    Nil->color = BLACK;
  }

  ~RBTree(){
    destroy(root);
    delete Nil;
    Nil = NULL;
  }
  void InOrder(){InOrder(root);}
  bool Insert(const Type& value);
  void Remove(Type key);
  void InOrderPrint(InOrderPrint(root);)

protected:
  RBTNode<Type>* BuyNode(const Type& x = Type());
  void InOrder(RBTNode<Type>* root);
  void LeftRotate(RBTNode<Type>* z);
  void RightRotate(RBTNode<Type>* z);
  void Insert_fixup(RBTNode<Type>* s);
  RBTNode<Type>* search(RBTNode<Type>* root, Type key) const;

private:
  RBTNode<Type>* root;
  RBTNode<Type>* Nil;
}

红黑树实现

红黑树插入

B-Tree

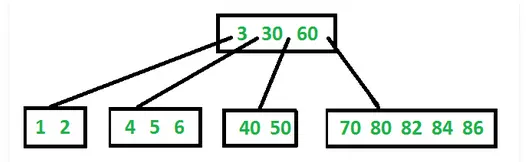
特点

所有的叶子都在同一层
B树由一个最小度t定义，t的值依赖于磁盘块的大小
所有的树节点除了根节点最少需要有t-1个关键字，根节点至少有一个关键字
所有的节点包括根节点都至多包含2t-1个关键字
节点的孩子数等于其关键字数+1
所有节点内的数字增序排列。在关键字K1和K2之间的所有子树上的节点关键字值都在K1和K2之间
B树的生长和收缩都是从根开始的，这点不同于其他的搜索树，其他的搜素树都是从底部开始生长和收缩的
像其他平衡的二叉搜索树一样，搜索插入和删除的时间复杂度是O(logn)

结点定义

class BTreeNode{
  int* keys;      // 关键字数组
  int t;          // 最小度
  BTreeNode** C;  // 对应孩子节点的数组指针
  int n;          // 节点当前关键字数量
  bool leaf;      // 是否是叶子节点

public:
  BTreeNode(int _t, bool _leaf);  // 构造函数
  void insertNonFull(int k);
  void traverse();  //遍历所有以该节点为根的子树的关键字
  void splitChild(int i, BTreeNode* y);
  BTreeNode* search(int k); //查询一个关键词在以该节点为根的子树

friend class BTree; //使其可以访问私有成员
};

BTree定义

class BTree{
  BTreeNode* root;
  int t;

public:
  BTree(int _t){
    root = NULL; t = _t;
  }
  void traverse(){
    if(root != NULL) root->traverse();
  }
  BTreeNode* search(int k)
    {  return (root == NULL)? NULL : root->search(k); }

  void insert(int k);
};

BTree方法

构造方法

void BTreeNode::BTreeNode(int _t, bool _leaf){
  t = _t;
  leaf = _leaf;
  
  keys = new int [2*t -1];
  C = new BTreeNode[2*t];

  n = 0;
}

遍历与查找方法

void BTreeNode::traverse(){
  int i;
  for(i = 0; i < n; i++){
    if(leaf == false)
      C[i] = ->traverse();
    cout << " " << keys[i];
  }
  if(leaf == false)
    C[i]->traverse();
}

BTreeNode* BTreeNode::search(int k){
  int i = 0;
  while(i < n && k >keys[i]){
    i++;
  }
  if(key[i] == k){
    return this;
  }
  if(leaf == true){
    return NULL;
  }
  return C[i]->search(k);
}

插入

void BTree::insert(int k){
  if(root == NULL){
    root = new BTreeNode(t, true);
    root->keys[0] = k;
    root->n = 1;
  }
  else {
    if(root->n == 2*t -1){

    }
    else
    root->insertNonFull(k);
  }
}

void BTreeNode::insertNonFull(int k){
  int i = n-1;
  if(leaf == true){

  }
}

B+Tree

LRU

上篇查找算法

下篇计算机网络基础