锁机制

CUDA锁函数`atomicCAS()`

接受参数

int / unsinged int
unsigned long long int
unsigned short int

锁机制模板类

template <typename T>
__device__ void atomic_max(T* addr, T val){
  atomicMax(addr, val);
}

template <typename T>
__device__ void atomic_add(T *addr, T val)
{
    atomicAdd(addr, val);
}
template <typename T>
__device__ void atomic_min(T *addr, T val)
{
    atomicMin(addr, val);
}

锁机制实现

__device__ __inline__ void atomic_max(int8_t* addr, int8_t val){
  if(*addr >= val)
    return;

  unsigned int* const addr_as_ull = (unsigned int*) addr;
  unsigned int old = *addr_as_ull;
  unsigned int assumed;
  do{
      assumed = old;
      if(reinterpret_cast<int8_t&>(assumed) >= val)
        break;
      old = atomicCAS(addr_as_ull, assumed, val);
  } while (assumed != old);
}

__device__ __inline__ void atomic_add(int8_t* addr, int8_t val){
  if(*addr >=val){
    return;
  }
  unsigned int* const addr_as_ull = (unsigned int*) addr;
  unsigned int old = *addr_as_ull;
  unsigned int assumed;
  do{
    assumed = old;
    old = atomicCAS(addr_as_ull, assumed, reinterpret_cast<int8_t&> (old) + val);
  }while(asuumed != old)
}

基础

快速整数除法

快速整数除法链接

array数据结构

array数据结构链接

channel shuffle 算子

基础

快速整数除法

步骤

论文链接 快速整数除法论文链接

代码实现

  #ifndef PPL_CUDA_DIVMOD_PAST_H_
  #define PPL_CUDA_DIVMOD_PAST_H_
  #include <stdint.h>
  #include <cuda_runtime.h>
  struct DivModFast{
    DivModFast(int d =1){
      d_ = (d==0) ? 1 : d;
      for(l_ = 0;;++l_){
        if((1U << l_) >= d_){
          break;
        }
      }
      uint64_t one = 1;
      uint64_t m = ((one << 32) * ((one << l_) - d_)) / d_ +1;
      m_ = static_cast<uint32_t> (m);
    }

  __device__ __inline__ int div(int index){
    uint tm = __umulhi(m_, index);
    (tm + index) >> l_;
  }
  __device__ __inline__ int mod(int idx) const
  {
    return idx - d_ * div(idx);
  }
  __divice__ __inline__  void divmod(int index, int& quo, int& rem){
      quo = div(index);
      rem = index - quo * d_;
    }

    uint32_t d_; // divisor
    uint32_t l_; // ceil(log2(d_))
    uint32_t m_; // m' in the paper

  }
  #endif

为什么需要定义一种类型为half8_

基础

NHWC和NCHW

它们在表示图像数据时的存储方式不同。
- NHWC表示图像的顺序为：（batch_size, height, width, channels），即批次大小、图像高度、图像宽度和通道数的顺序
- NCHW表示图像的顺序为：（batch_size, channels, height, width），即批次大小、通道数、图像高度和图像宽度的顺序
NCHW通常更适合GPU的并行计算方式
- 更好利用GPU的内存布局和数据传输特性
NHWC通常更适合CPU的计算方式
- 符合CPU的内存层次结构和缓存策略

什么是带stride的算子方法

在计算机视觉和深度学习中，带有stride的算子方法通常用于处理图像或其他类型的多维数据
Stride是指在多维数组中，沿着每个轴或维度的间隔（或跳过）的元素数
- 带有stride的算子方法会根据输入和输出的内存布局以及stride参数，计算每个元素的位置，以便在处理多维数据时能够正确地访问每个元素
- 例如，如果一个算子需要处理一个四维张量（例如图像），则它需要知道每个维度的步长，以便能够正确地遍历整个张量
- 使用带有stride的算子方法可以大大简化计算多维数据的代码，并且可以加速算法的执行速度

带stride的算子方法为什么能够加速

通过对输入和输出数据的内存地址进行计算，从而在一个线程块中对多个数据进行计算。
带stride的算子方法可以将输入数据中每个数据的访问间隔设置为固定值，从而能够更好地利用CPU或GPU的cache机制，提高数据的缓存命中率，进一步提高计算效率。

SQL

选择数据

SELECT

选择表中的数据

  SELECT col1 from mytable;

JOIN / LEFT JOIN / RIGHT JOIN & UNION

选择多张表中数据

  SELECT table.col1, table.col2, table_else.col3 FROM
  (SELECT col1, col2 FROM mytable) table
  JOIN
  (SELECT col1, col3 FROM mytable_else) table_else
  ON
  table.col1 = table_else.col1;

JOIN 类型

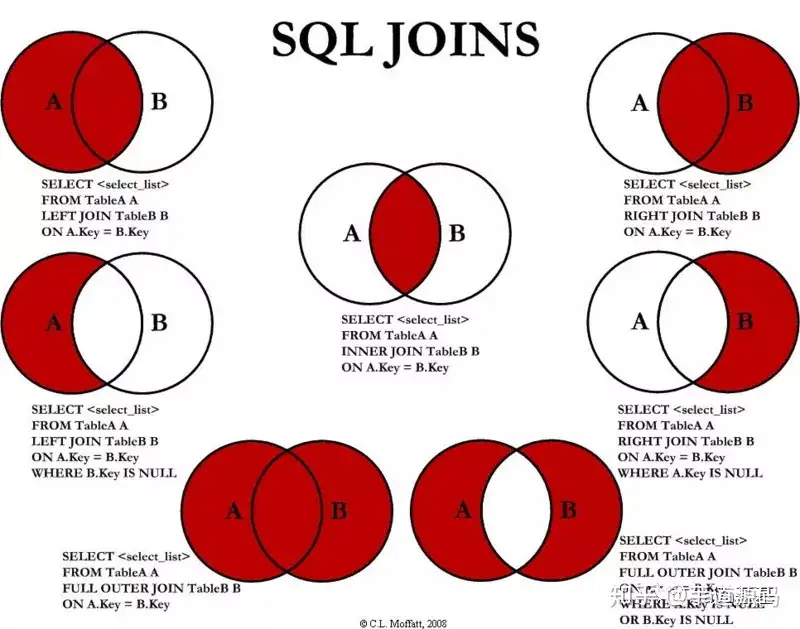LEFT JOIN ON（左上） RIGHT JOIN ON（右上） JOIN / INNER JOIN ON（中） FULL OUTER JOIN ON（左下）

347 209 3 5 968

110 235 236 51 37 376 45 1005 416 1049 494 474 518 377 322 279 139 115

1002. 查找常用字符

class Solution {
public:
    vector<string> commonChars(vector<string>& words) {
        vector<int> minfreq(26, INT_MAX);
        vector<int> freq(26);
        for (const string& word: words) {
            fill(freq.begin(), freq.end(), 0);
            for (char ch: word) {
                ++freq[ch - 'a'];
            }
            for (int i = 0; i < 26; ++i) {
                minfreq[i] = min(minfreq[i], freq[i]);
            }
        }

        vector<string> ans;
        for (int i = 0; i < 26; ++i) {
            for (int j = 0; j < minfreq[i]; ++j) {
                ans.emplace_back(1, i + 'a');
            }
        }
        return ans;
    }
};

349. 两个数组的交集

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> set1, set2;
        for (auto& num : nums1) {
            set1.insert(num);
        }
        for (auto& num : nums2) {
            set2.insert(num);
        }
        return getIntersection(set1, set2);
    }

    vector<int> getIntersection(unordered_set<int>& set1, unordered_set<int>& set2) {
        if (set1.size() > set2.size()) {
            return getIntersection(set2, set1);
        }
        vector<int> intersection;
        for (auto& num : set1) {
            if (set2.count(num)) {
                intersection.push_back(num);
            }
        }
        return intersection;
    }
};

202. 快乐数

class Solution {
public:
    bool isHappy(int n) {
        unordered_set<int> set;
        int res = n;
        while (true) {
            res = square(res);
            if (res == 1) {
                return true;
            }
            if (set.find(res)!=set.end()) {//找到返回迭代器，失败返回end
                return false;
            }
            set.insert(res);
            
        }    
    }

    int square(int n) {
        int sum = 0, temp = 1;
        while (n != 0) {
            temp = n % 10;
            sum += temp * temp;
            n /= 10;
        }
        return sum;
    }
};

454. 四数相加 II

class Solution {
public:
    int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {
        unordered_map<int, int> countAB;
        for (int u: A) {
            for (int v: B) {
                ++countAB[u + v];
            }
        }
        int ans = 0;
        for (int u: C) {
            for (int v: D) {
                if (countAB.count(-u - v)) {
                    ans += countAB[-u - v];
                }
            }
        }
        return ans;
    }
};

18. 四数之和

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> quadruplets;
        if (nums.size() < 4) {
            return quadruplets;
        }
        sort(nums.begin(), nums.end());
        int length = nums.size();
        for (int i = 0; i < length - 3; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            if ((long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
                break;
            }
            if ((long) nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
                continue;
            }
            for (int j = i + 1; j < length - 2; j++) {
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                if ((long) nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
                    break;
                }
                if ((long) nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
                    continue;
                }
                int left = j + 1, right = length - 1;
                while (left < right) {
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum == target) {
                        quadruplets.push_back({nums[i], nums[j], nums[left], nums[right]});
                        while (left < right && nums[left] == nums[left + 1]) {
                            left++;
                        }
                        left++;
                        while (left < right && nums[right] == nums[right - 1]) {
                            right--;
                        }
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        right--;
                    }
                }
            }
        }
        return quadruplets;
    }
};

383. 赎金信

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        if (ransomNote.size() > magazine.size()) {
            return false;
        }
        vector<int> cnt(26);
        for (auto & c : magazine) {
            cnt[c - 'a']++;
        }
        for (auto & c : ransomNote) {
            cnt[c - 'a']--;
            if (cnt[c - 'a'] < 0) {
                return false;
            }
        }
        return true;
    }
};

数学

6. N 字形变换

class Solution {
public:
	string convert(string s, int numRows) {

		if (numRows == 1) return s;

		vector<string> rows(min(numRows, int(s.size()))); // 防止s的长度小于行数
		int curRow = 0;
		bool goingDown = false;

		for (char c : s) {
			rows[curRow] += c;
			if (curRow == 0 || curRow == numRows - 1) {// 当前行curRow为0或numRows -1时，箭头发生反向转折
				goingDown = !goingDown;
			}
			curRow += goingDown ? 1 : -1;
		}

		string ret;
		for (string row : rows) {// 从上到下遍历行
			ret += row;
		}

		return ret;
	}
};

7. 整数反转

class Solution {
public:
    int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            rev = rev * 10 + digit;
        }
        return rev;
    }
};

哈希表

1. 两数之和

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map <int,int> map;
        for(int i = 0 ; i < nums.size(); i++){
            auto num = map.find(target - nums[i]);
            if(num != map.end()){
                return {i, num->second};
            }
            map[nums[i]] = i;
        }
        return {};
    }
};

242. 有效的字母异位词

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.length() != t.length()) {
            return false;
        }
        vector<int> table(26, 0);
        for (auto& ch: s) {
            table[ch - 'a']++;
        }
        for (auto& ch: t) {
            table[ch - 'a']--;
            if (table[ch - 'a'] < 0) {
                return false;
            }
        }
        return true;
    }
};

字符串

344.反转字符串

class Solution {
public:
    void reverseString(vector<char>& s) {
        int n = s.size();
        for (int left = 0, right = n - 1; left < right; ++left, --right) {
            swap(s[left], s[right]);
        }
    }
};

541.反转字符串II

class Solution {
public:
    string reverseStr(string s, int k) {
        int n = s.length();
        for (int i = 0; i < n; i += 2 * k) {
            reverse(s.begin() + i, s.begin() + min(i + k, n));
        }
        return s;
    }
};

15. 三数之和

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    ans.push_back({nums[first], nums[second], nums[third]});
                }
            }
        }
        return ans;
    }
};

剑指offer 05: 替换空格

class Solution {
public:
    string replaceSpace(string s) {
        int count = 0, len = s.size();
        // 统计空格数量
        for (char c : s) {
            if (c == ' ') count++;
        }
        // 修改 s 长度
        s.resize(len + 2 * count);
        // 倒序遍历修改
        for(int i = len - 1, j = s.size() - 1; i < j; i--, j--) {
            if (s[i] != ' ')
                s[j] = s[i];
            else {
                s[j - 2] = '%';
                s[j - 1] = '2';
                s[j] = '0';
                j -= 2;
            }
        }
        return s;
    }
};

剑指 Offer 58 - II. 左旋转字符串

//方法1---借助额外字符串
class Solution {
public:
    string reverseLeftWords(string s, int n) {
        string ans = s;
        int length = s.size();
        for(int i=0;i<length;i++)
        {
            ans[(i+length-n)%length] = s[i];
        }
        return ans;
    }
};

28. 找出字符串中第一个匹配项的下标

class Solution {
public:
    int strStr(string haystack, string needle) {
        int n = haystack.size(), m = needle.size();
        if (m == 0) {
            return 0;
        }
        vector<int> pi(m);
        for (int i = 1, j = 0; i < m; i++) {
            while (j > 0 && needle[i] != needle[j]) {
                j = pi[j - 1];
            }
            if (needle[i] == needle[j]) {
                j++;
            }
            pi[i] = j;
        }
        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack[i] != needle[j]) {
                j = pi[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }
};

459. 重复的子字符串

class Solution {
public:
    void getNext (int* next, const string& s){
        next[0] = 0;
        int j = 0;
        for(int i = 1;i < s.size(); i++){
            while(j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if(s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern (string s) {
        if (s.size() == 0) {
            return false;
        }
        int next[s.size()];
        getNext(next, s);
        int len = s.size();
        if (next[len - 1] != 0 && len % (len - (next[len - 1] )) == 0) {
            return true;
        }
        return false;
    }
};

栈与队列

232. 用栈实现队列

class MyQueue {
private:
    stack<int> inStack, outStack;

    void in2out() {
        while (!inStack.empty()) {
            outStack.push(inStack.top());
            inStack.pop();
        }
    }

public:
    MyQueue() {}

    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            in2out();
        }
        int x = outStack.top();
        outStack.pop();
        return x;
    }

    int peek() {
        if (outStack.empty()) {
            in2out();
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};

[225. 用队列实现栈]

class MyStack {
public:
    queue<int> queue1;
    queue<int> queue2;

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        queue2.push(x);
        while (!queue1.empty()) {
            queue2.push(queue1.front());
            queue1.pop();
        }
        swap(queue1, queue2);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int r = queue1.front();
        queue1.pop();
        return r;
    }
    
    /** Get the top element. */
    int top() {
        int r = queue1.front();
        return r;
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return queue1.empty();
    }
};

151. 翻转字符串里的单词

class Solution {
public:
    string reverseWords(string s) {
        int left = 0, right = s.size() - 1;
        // 去掉字符串开头的空白字符
        while (left <= right && s[left] == ' ') ++left;

        // 去掉字符串末尾的空白字符
        while (left <= right && s[right] == ' ') --right;

        stack<string> d;
        string word;

        while (left <= right) {
            char c = s[left];
            if (word.size() && c == ' ') {
                // 将单词 push 到队列的头部
                d.push(word);
                word = "";
            }
            else if (c != ' ') {
                word += c;
            }
            ++left;
        }
        d.push(word);
        
        string ans;
        while (!d.empty()) {
            ans += d.top();
            d.pop();
            if (!d.empty()) ans += ' ';
        }
        return ans;
    }
};

20. 有效的括号

class Solution {
public:
    bool isValid(string s) {
        // 设置unordered_map m，对应(为1，[为2，{为3，)为4，]为5，}为6
        stack<char> st;
        bool istrue=true;
        for(char c:s){
            int flag=m[c];
            if(flag>=1&&flag<=3) st.push(c);
            else if(!st.empty()&&m[st.top()]==flag-3) st.pop();
            else {istrue=false;break;}
        }
        if(!st.empty()) istrue=false;
        return istrue;
    }
};

150. 逆波兰表达式求解

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> stk;
        int n = tokens.size();
        for (int i = 0; i < n; i++) {
            string& token = tokens[i];
            if (isNumber(token)) {
                stk.push(atoi(token.c_str()));
            } else {
                int num2 = stk.top();
                stk.pop();
                int num1 = stk.top();
                stk.pop();
                switch (token[0]) {
                    case '+':
                        stk.push(num1 + num2);
                        break;
                    case '-':
                        stk.push(num1 - num2);
                        break;
                    case '*':
                        stk.push(num1 * num2);
                        break;
                    case '/':
                        stk.push(num1 / num2);
                        break;
                }
            }
        }
        return stk.top();
    }

    bool isNumber(string& token) {
        return !(token == "+" || token == "-" || token == "*" || token == "/");
    }
};

239. 滑动窗口最大值

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        priority_queue<pair<int, int>> q;
        for (int i = 0; i < k; ++i) {
            q.emplace(nums[i], i);
        }
        vector<int> ans = {q.top().first};
        for (int i = k; i < n; ++i) {
            q.emplace(nums[i], i);
            while (q.top().second <= i - k) {
                q.pop();
            }
            ans.push_back(q.top().first);
        }
        return ans;
    }
};

347. 前K个高频元素

class Solution {
public:


    static bool cmp(pair<int, int>&m, pair<int, int> & n){
        return m.second > n.second;
    }

    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int,int> map;
        for(int i = 0 ; i <nums.size(); i++){
            map[nums[i]]++;
        }
        priority_queue<pair<int,int>, vector<pair<int,int>>, decltype(&cmp)> q(cmp);

        for(auto& [num, count] : map){
            if(q.size() == k){
                if(q.top().second < count){
                    q.pop();
                    q.emplace(num, count);
                }
            }else{
                q.emplace(num, count);
            }
        }
        vector<int> res;
        while(!q.empty()){
            res.emplace_back(q.top().first);
            q.pop();
        }
        return res;
    }
};

1047. 删除字符串中的所有相邻重复项

class Solution {
public:
    string removeDuplicates(string s) {
        string stk;
        for (char ch : s) {
            if (!stk.empty() && stk.back() == ch) {
                stk.pop_back();
            } else {
                stk.push_back(ch);
            }
        }
        return stk;
    }
};

数组

704. 二分查找

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right){
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

27. 移除元素

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int n = nums.size();
        int left = 0;
        for (int right = 0; right < n; right++) {
            if (nums[right] != val) {
                nums[left] = nums[right];
                left++;
            }
        }
        return left;
    }
};

977. 有序数组的平方

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> ans;
        for (int num: nums) {
            ans.push_back(num * num);
        }
        sort(ans.begin(), ans.end());
        return ans;
    }
};

209. 长度最小的子数组

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

59. 螺旋矩阵II

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int maxNum = n * n;
        int curNum = 1;
        vector<vector<int>> matrix(n, vector<int>(n));
        int row = 0, column = 0;
        // 设置方向为右下左上vector<vector<int>> directions = {0,1}等
        int directionIndex = 0;
        while (curNum <= maxNum) {
            matrix[row][column] = curNum;
            curNum++;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= n || nextColumn < 0 || nextColumn >= n || matrix[nextRow][nextColumn] != 0) {
                directionIndex = (directionIndex + 1) % 4;  // 顺时针旋转至下一个方向
            }
            row = row + directions[directionIndex][0];
            column = column + directions[directionIndex][1];
        }
        return matrix;
    }
};

滑动窗口

3. 无重复最长子串

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        // 哈希集合，记录每个字符是否出现过
        unordered_set<char> occ;
        int n = s.size();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        // 枚举左指针的位置，初始值隐性地表示为 -1
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.erase(s[i - 1]);
            }
            while (rk + 1 < n && !occ.count(s[rk + 1])) {
                // 不断地移动右指针
                occ.insert(s[rk + 1]);
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = max(ans, rk - i + 1);
        }
        return ans;
    }
};

11. 盛最多水的容器

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                max(res, (j - i) * height[i++]): 
                max(res, (j - i) * height[j--]); 
        }
        return res;
    }
};

42. 接雨水

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        vector<int> maxLeft(height.size(), 0);
        vector<int> maxRight(height.size(), 0);
        int size = maxRight.size();

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i < size; i++) {
            maxLeft[i] = max(height[i], maxLeft[i - 1]);
        }
        // 记录每个柱子右边柱子最大高度
        maxRight[size - 1] = height[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            maxRight[i] = max(height[i], maxRight[i + 1]);
        }
        // 求和
        int sum = 0;
        for (int i = 0; i < size; i++) {
            int count = min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
};

84. 柱状图中最大的矩形

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        vector<int> minLeftIndex(heights.size());
        vector<int> minRightIndex(heights.size());
        int size = heights.size();

        // 记录每个柱子 左边第一个小于该柱子的下标
        minLeftIndex[0] = -1; // 注意这里初始化，防止下面while死循环
        for (int i = 1; i < size; i++) {
            int t = i - 1;
            // 这里不是用if，而是不断向左寻找的过程
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        // 记录每个柱子 右边第一个小于该柱子的下标
        minRightIndex[size - 1] = size; // 注意这里初始化，防止下面while死循环
        for (int i = size - 2; i >= 0; i--) {
            int t = i + 1;
            // 这里不是用if，而是不断向右寻找的过程
            while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }
        // 求和
        int result = 0;
        for (int i = 0; i < size; i++) {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            result = max(sum, result);
        }
        return result;
    }
};

动态规划

5. 最长回文子串

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        vector<vector<int>> dp(n, vector<int>(n));
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= n; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < n; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= n) {
                    break;
                }

                if (s[i] != s[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substr(begin, maxLen);
    }
};

链表

707. 设计链表

class MyLinedList(){
private:
    int size;
    ListNode* head;
public:
    MyLinedList(){
        this->size = 0;
        this->head = new ListNode(0);
    }
    int get(int index){
        if(index<0 || index >= size){
            return 0;
        }
        ListNode* cur = head;
        for(int cur_index = 0; cur_index <= index;cur_index++){
            cur = cur->next;
        }
        return cur->val;
    }
    int add_at_head(int val){
        add_at_index(0,val);
    }
    int add_at_tail(int val){
        add_at_index(size,val);
    }
    void add_at_index(int index, int val){
        if(index < 0 || index > size){
            return;
        }
        size++;
        ListNode* pre = head;
        ListNode* newone = new ListNode(val);

        for(int i = 0 ; i<index; i++){
            pre = pre->next;
        }
        newone->next = pre->next;
        pre->next = newone;
    }
    void delete_at_index(int index){
        if(index < 0 || index >= size){
            return;
        }
        ListNode* pre = head;
        for(int i = 0 ; i <index; i++){
            pre = pre->next;
        }
        ListNode* deleteone = pre->next;
        pre->next = pre->next->next;
        delete deleteone;
}
}

2. 两数相加

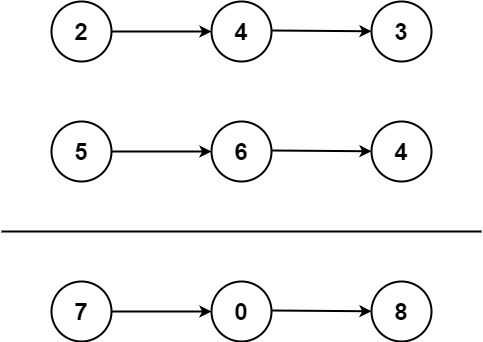
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *head = nullptr, *tail = nullptr;
        int carry = 0;
        while (l1 || l2) {
            int n1 = l1 ? l1->val: 0;
            int n2 = l2 ? l2->val: 0;
            int sum = n1 + n2 + carry;
            if (!head) {
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }
            carry = sum / 10;
            if (l1) {
                l1 = l1->next;
            }
            if (l2) {
                l2 = l2->next;
            }
        }
        if (carry > 0) {
            tail->next = new ListNode(carry);
        }
        return head;
    }
};

203. 移除链表元素

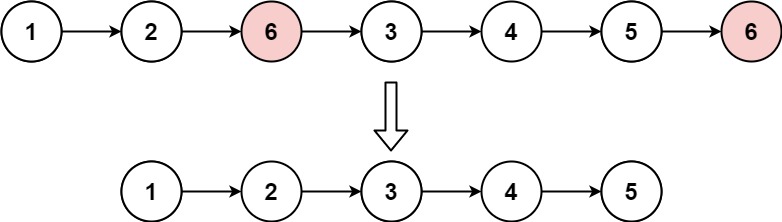
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) {
            return head;
        }
        head->next = removeElements(head->next, val);
        return head->val == val ? head->next : head;
    }
};

Shared memory

Basic

与global memory 区别

为片上内存，SRAM实现
SRAM 支持随机存储，不需要global memory 的burst 存取
延迟
比global memory低20/30倍，带宽大10倍
shared memory不管是否有没有bank conflict问题，都比global memory要快很多
有些时候为了避免bank conflict从而做了很多优化，但是由于额外的增加intrinsic，导致perf反而变差

什么时候使用

数据有复用的话，考虑使用shared memory

使用时需要注意

使用shared memory解决了global memory中的对齐和合并以及非原子操作的顺序问题，但存在bank conflict的问题，使用时要注意不要忘记synchronize的使用
从Volta开始，warp内部不是lock step的，所以warp内部使用shared memory有时候也需要memory fence
shared memory使用后，应当考虑一个sm能有多少个thread和block

从global memory到shared memory的加载过程

global memory -> cache (optional L1)L2 -> per thread register -> shared memory
不经过register的方法(CUDA11有async，不经过register的方法，see below section)

使用shared memory用于计算

首先从shared memory 读取数据，放到tmp register 上，然后在register 上计算，最终再把结果从register 放到对应目的地。
计算中的latency来自从shared memory到register

shared memory & occupancy

occupancy:
每个SM的活动wrap与最大可能活动warp的比值，其表征了系统性能。
shared memory 提高可能对occupancy产生负面影响(限制SM的occupancy的因素包括warp个数、block个数、register个数、shared memory数量、block中register & shared memory大小)
- 在很多现实场景中，不再采用shared memory与threads一对一的关系，一个shared memory大小为64*64，block最大thread为1024，则采用 32*32的thread个数，然后一个thread处理4个elements，该种方法性能同样可以提高。
- 评估
  occupancy对性能的影响程度通过动态分配shared 来实验，在配置的第三个参数中指定，增加此参数，可以有效减少内核占用率，测量对性能的影响。

occupancy

每个SM的活动wrap与最大可能活动warp的比值
线程块大小：较小的线程块可以更好地利用 GPU 的资源，因为 GPU 上的资源是按线程块来分配的。通常来说，线程块大小越小，GPU 可用资源的利用率就越高。
寄存器使用：每个线程块在运行时需要使用一定数量的寄存器来保存中间结果和变量。寄存器的数量是有限的，当线程块使用的寄存器数量过多时，就会导致 GPU 上可以同时运行的线程块数量减少，从而降低 GPU occupancy。
共享内存使用：共享内存是一种高速缓存，能够在线程块内部共享数据。但是，共享内存的大小也是有限的，当线程块使用的共享内存过多时，就会导致 GPU 上可以同时运行的线程块数量减少，从而降低 GPU occupancy。
全局内存访问：全局内存是 GPU 上的主要存储区域，但是访问全局内存需要消耗大量的时间和资源。当线程块频繁地访问全局内存时（需要等待），就会导致 GPU 上可以同时运行的线程块数量减少，从而降低 GPU occupancy。
硬件限制：每个 GPU 都有自己的硬件限制，包括寄存器数量、共享内存大小、带宽等等。当线程块使用的资源超过了硬件的限制时，就会导致 GPU 上可以同时运行的线程块数量减少，从而降低 GPU occupancy。

API

dynamic use

只分配1D
比起使用static shared memory，dynamic shared memory有一些小的overhead。

   extern __shared__ int tile[];

   MyKernel<<<blocksPerGrid, threadsPerBlock, isize*sizeof(int)>>>(...);

static use

1/2/3D

   __shared__ float a[size_x][size_y];

shared memory位置

cc 2.x、cc 3.x、cc 7.x、cc 8.x、cc 9.x、L1和shared memory一块配置
cc 5.x、cc 6.x L1和 texture memory 一块配置，shared memory有自己的空间

shared memory配置

L1 + Shared 一共有64 kb memory (在某些device上)
- shared memory使用32 bank访问。L1 cache使用cache line来访问。
- 如果kernel使用很多shared memory，prefer larger shared memory

* 如果kernel使用<font color = red>很多register</font>，prefer larger L1 cache。因为register会spilling to L1 cache

shared memory配置 API

设置device

   cudaError_t cudaDeviceSetCacheConfig(cudaFuncCache cacheConfig);

设置可选项

如果当前kernel的setting与前一个kernel的不一样，可能会导致implicit sync with device

设置func

   cudaError_t cudaFuncSetCacheConfig(const void* func, enum cudaFuncCacheca cheConfig);

如果当前内核的设置与前一内核不一样，可能会导致implicit sync with device

Memory Bank

Shared memory & transaction

shared memory 与global memory 类似，以warp 为单位进行读写。warp 内的多个thread 首先会合并为一个或多个transaction，然后访问shared memory。增加数据的利用率，减少总访问次数。
- 最好的情况
  只会引发一次transaction。最坏的情况引发32次transaction。
- 如果都访问同一地址，则只产生一次transaction，然后broadcast到每一个threads。同样的broadcast在使用constant cache，warp level shuffle的时候都有。
在warp操作shared memory中，如果load/store指令在每个bank只有一块数据，且数据小于bank带宽，则可充分利用每个bank自己的带宽。
- 最好的使用
  shared memory的办法就是确保请求的数据分布在每个bank中，每个bank充分的利用bank自己的bandwidth

Memory bank & bank conflict

特点

shared memory底层被切分为多个banks 来使用。可以同时访问使用多个banks，shared memory带宽为bank的n倍。
对于shared memory的多个访问如果都落到一个bank中不是same word，则request会被replay。将一次request转化为serialized requests。(图 21 中间)。花费的时间：num replay * one bank free time
如果多个thread的内存请求到相同bank的same word，访问不会serialize。如果是read则会broadcast，如果是write则只要一个thread写，但是哪个thread写不确定。bandwidth的使用依旧很低，因为num banks * bank bandwidth这么多的数据只用于传送一个word的数据。

三种访问shared memory方法

parallle access
: 没有bank conflict
serial access
: 带有bank conflict触发serialized access
broadcast access
: 现有单个读当前的bank的word，之后进行broadcast到所有warp内的threads中

Access Mode 32/64-bit

定义

shared memory bank width
: defines shared memory 地址和shared memory bank 之间的映射关系。

分类

32 bits
for 除了 cc 3.x之外的版本
64-bits
for cc 3.x

32 bits

一共32 banks，每个bank 32 bits
。 $ bank \ index=(byte \ address / 4 \ bytes)\% \ 32 \ banks $
下图word index 为 bytes address 对应的word index，然后从word index 对应到bank index

64 bits

一共32 banks，每个bank 64 bit，word大小由32/64 bits。
word大小为64 bits中
，
- 有32 banks，每个bank 64 bits，bytes的分割以8 bytes为单位分隔 $ bank \ index=(byte \ address / 8 \ bytes)\% \ 32 \ banks $
- 当thread 查询/写入word子字时，发生boradcast或write undifined
word大小为32 bits中
，
- 有32 banks，每个bank 64 bits，bytes的分割以4 bytes为单位分隔。 $ bank \ index=(byte \ address / 4 \ bytes)\% \ 32 \ banks $
- 32-bit mode下，访问同一个bank的2个32-bit word不一定产生bank conflict，因为bank width是64，可以把2个word都传送出去。
- bank conflict的本质：是bank width小，所以无法传送过多的数据
- 当thread 查询/写入word时，发生boradcast或write undifined

bank width对性能的影响 bank width提高会带来更大的带宽，但是会有更多的bank conflict

配置cc 3.x及以上版本的API

改变Kepler下shared memory bank可能会导致implicit sync with device

   // query access mode 
   cudaError_t cudaDeviceGetSharedMemConfig(cudaSharedMemConfig *pConfig);

   cudaSharedMemBankSizeFourByte
   cudaSharedMemBankSizeEightByte

   // setting access mode
   cudaError_t cudaDeviceSetSharedMemConfig(cudaSharedMemConfig config);
   cudaSharedMemBankSizeDefault 
   cudaSharedMemBankSizeFourByte 
   cudaSharedMemBankSizeEightByte

Stride access

stride access

对于global memory是waste bandwith，同时解决了对齐问题。
对于shared memory是解决bank conflict的方法。

stride在shared memory

stride定义：warp连续thread访问内存的间隔。

如果t0访问float array idx0，t1访问float array idx1，则stride of one 32 bit word

不同的stride，对应的conflict类型不同 (假设2.x 32-bit mode)
- stride of one 32 bit word : conflict free
- stride of two 32 bit word : 16 x 2-way (2-way表示会被serialize为两个access) bank conflict
- stride of three 32 bit word : conflict free
- stride of 32 32 bit word : 1 x 32-way (32-way表示会被serialize为32个access) bank conflict
对于32 bits mode，奇数的stride是conflict free的，偶数的stride是有conflict

Avoid bank conflict

stride of 32 32 bits word (32-bit mode)

stride of 32 32 bits word 产生 1 x 32-way bank conflict 经常发生在使用shared memory处理2D array of 32 x 32，每个thread负责一个row。这样每个thread对应的row开始都会是在同一个bank中。
解决方法是pad 2d array to size 32 x 33, 这样每个thread负责的一个row的开始都不是在一个bank中 (stride of 33 33 bit word是conflict free的)

对于padding 64-bit与32-bit mode的方法是不一样。有些在32-bit上是conflict free的，在64-bit上就有conflict了

stride of 1 32 bits words

满足coarlesed global memory access & shared memory conflict free。

global memory noncolaesced 和bank conflict冲突

当发生冲突时，如果对shared memory操作更多则先解决bank conflict，然后再考虑noncolaesced，但同样得需要做benchmark

Data Layout

Square Shared Memory

  __shared__ int tile[N][N];

  // contigious thread access row of shared memory (contigious)
  tile[threadIdx.y][threadIdx.x];

  // contigious thread access col of shared memory (stride)
  tile[threadIdx.x][threadIdx.y];

padding

   __shared__ int tile[BDIMY][BDIMX+1];

Rectangle Shared Memory

  #define BDIMX 32 // 32 col
  #define BDIMY 16 // 16 row

  dim3 block (BDIMX,BDIMY); 
  dim3 grid (1,1);

  // row-major read (setRowReadRow)
  // the length of the innermost dimension of the shared memory array tile is set to the same dimension as the innermost dimension of the 2D thread block:
  // contigious thread read row of shared memory (contigious)
  __shared__ int tile[BDIMY][BDIMX];


  // col-major read (setColReadCol)
  // the length of the innermost dimension of the shared memory array tile is set to the same dimension as the outermost dimension of the 2D thread block:
  // contigious thread read col of shared memory (stride)
  __shared__ int tile[BDIMX][BDIMY];

举例

配置

计算 word：32 bits，bank 64bits，对列主序来说16*32/64 = 8 bank -> a column are arranged into eight banks.
列主序代码

```cpp
__global__ void setRowReadCol(int *out) { 
  // static shared memory
  __shared__ int tile[BDIMY][BDIMX];
  // mapping from 2D thread index to linear memory
  unsigned int idx = threadIdx.y * blockDim.x + threadIdx.x;
  // convert idx to transposed coordinate (row, col) 
  unsigned int irow = idx / blockDim.y;
  unsigned int icol = idx % blockDim.y;
  // shared memory store operation 
  tile[threadIdx.y][threadIdx.x] = idx;
  // wait for all threads to complete 
  __syncthreads();
  // shared memory load operation
  out[idx] = tile[icol][irow]; 
}
```

padding

对于32-bit bank，padding 1
对于64-bit bank，padding取决于data
在上面的例子里，padding 2 element for 64-bit bank

   #define NPAD 2
   __shared__ int tile[BDIMY][BDIMX + NPAD];

Corner-Turning

定义

Corner-Turning是一种在GPU计算中用于优化内存访问模式的技术。它的原理是将数据在内存中重新排列，原本分散在内存中的数据按照每个线程块可以同时访问一段连续的内存而整理到一起，使得每个线程块内部的访问就可以利用GPU的内存带宽，从而提高计算性能

特点与性能分析

排列后的数据可以被看作是一个多维数组，由于其存储方式的改变，数据在访问时也需要进行一定的转换。

在某些情况下可以显著提高性能，但在其他情况下可能导致性能下降。需要仔细评估其适用性，并进行充分的测试和调优。

例子

待排序二维数组A，大小为M x N，其中M表示行数，N表示列数
使用一个大小为P x Q的线程块来处理A
- 为了最大程度地利用GPU的内存带宽，使用 Corner-Turning 将A重新排列为一个大小为P x (M/P) x Q x (N/Q)的四维数组B。其中，每个线程块可以处理B中的一个二维子数组。
  - 将A中的每个元素按照其所在行和列的顺序依次存储到一个一维数组C中。即，C[0]表示A[0][0]，C[1]表示A[0][1]，C[N]表示A[1][0]，以此类推。
  - 将C中的元素按照一定的方式重新排列，使得相邻的P个元素在行上连续。C[0], C[N], C[2N], ..., C[(M/P-1)N] // 第一个线程块处理的数据、C[1], C[N+1], C[2N+1], ..., C[(M/P-1)N+1]、...、C[P-1], C[N+P-1], C[2N+P-1], ..., C[(M/P-1)N+P-1]
  - 将排列后的元素存储到B中。具体而言，将C中的前P*(M/P)个元素依次存储到B的第一维中，每个线程块处理的数据存储在B的第二维和第四维中。
  - B[i][j][k][l] = C[i*(M/P)N + jN + k*Q + l]
  - 每个线程块可以同时访问B中的一个大小为(M/P) x (N/Q)的子数组，从而最大程度地利用GPU的内存带宽。

Example GEMM data access

当使用tilnig+每个thread读取一个M N到shared memory的时候，读取M也是burst的。这是因为比起上面的simple code使用iteration读取，这里使用多个thread读取，一次burst的数据会被临近的thread使用(M00 M01分别被2个thread读取，每个thread只读取一个M elem)，而不是下一个iteration被清空。

这里对于M没有使用显性的memory transpose，但是因为使用多个thread读取数据，依旧保证了burst，这与CPU代码需要使用transpose是不一样的。

同时shared memory使用的是SRAM，不像DRAM有burst的问题，所以读取M的shared memory的时候尽管不是连续读取也没有问题。shared memories are implemented as intrinsically high-speed on-chip memory that does not require coalescing to achieve high data access rate.

Async global memory to shared memory

支持版本 CUDA 11.0

优点

将数据复制与计算重合
避免使用中间寄存器，减少寄存器压力，减少指令流水压力，提高内核占用率
相对于sync，async延迟更少

async与Cache关系

可以选择是否使用L1 cache
.
因为shared memory是per SM的，所以不涉及使用L2 cache(across SM)

优化参考图

对于sync拷贝，num data是multiply of 4 最快
对于async拷贝，data size是8/16是最快的。

例子

  template <typename T>
  __global__ void pipeline_kernel_sync(T *global, uint64_t *clock, size_t copy_count) {
    extern __shared__ char s[];
    T *shared = reinterpret_cast<T *>(s);

    uint64_t clock_start = clock64();

    for (size_t i = 0; i < copy_count; ++i) {
      shared[blockDim.x * i + threadIdx.x] = global[blockDim.x * i + threadIdx.x];
    }

    uint64_t clock_end = clock64();

    atomicAdd(reinterpret_cast<unsigned long long *>(clock),
              clock_end - clock_start);
  }

  template <typename T>
  __global__ void pipeline_kernel_async(T *global, uint64_t *clock, size_t copy_count) {
    extern __shared__ char s[];
    T *shared = reinterpret_cast<T *>(s);

    uint64_t clock_start = clock64();

    //pipeline pipe;
    for (size_t i = 0; i < copy_count; ++i) {
      __pipeline_memcpy_async(&shared[blockDim.x * i + threadIdx.x],
                              &global[blockDim.x * i + threadIdx.x], sizeof(T));
    }
    __pipeline_commit();
    __pipeline_wait_prior(0);
    
    uint64_t clock_end = clock64();

    atomicAdd(reinterpret_cast<unsigned long long *>(clock),
              clock_end - clock_start);
  }

API

__pipeline_memcpy_async()

代码将global memory数据存储到shared memory

__pipeline_wait_prior(0)

等待，直到剩余0条指令未执行

共计 41 篇文章，6 页。

锁机制

CUDA锁函数atomicCAS()

锁机制模板类

锁机制实现

基础

快速整数除法

array数据结构

channel shuffle 算子

基础

快速整数除法

基础

SQL

选择数据

SELECT

JOIN / LEFT JOIN / RIGHT JOIN & UNION

JOIN 类型

数学

哈希表

字符串

栈与队列

[225. 用队列实现栈]

数组

滑动窗口

动态规划

链表

Shared memory

Basic

API

Memory Bank

Shared memory & transaction

Memory bank & bank conflict

Access Mode 32/64-bit

32 bits

64 bits

Stride access

Avoid bank conflict

Data Layout

Square Shared Memory

Rectangle Shared Memory

Corner-Turning

定义

特点与性能分析

例子

Example GEMM data access

Async global memory to shared memory

例子

API

CUDA锁函数`atomicCAS()`